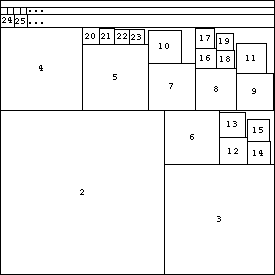

For convenience, we have labelled a square n if it has side length 1/n . Similarly, we will call it square n in what follows. The positions of all the larger squares are shown. Squares 24, 25, . . . 47 are arranged in a row. Squares 48, 49, . . . 95 are arranged in a row above that, and so on.
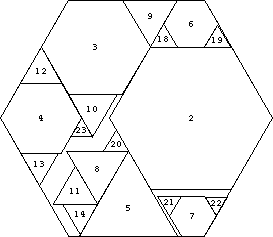
The same sort of packing can be done for triangles.

We can also do it for hexagons. The triangles stand for an infinite regress of hexagons. For example, the triangle labelled 5 contains hexagons (5), (15, 16, 17), (45, 46, 47, 48, 49, 50, 51, 52, 53), and so on.