Spiral Galaxies Puzzles are NP-complete

Erich Friedman
Stetson University, DeLand, FL 32723
efriedma@stetson.edu

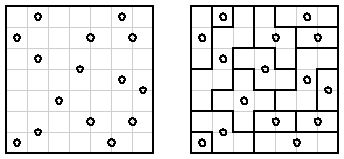
Introduction

Spiral Galaxies puzzles are pencil and paper puzzles which originated in Japan. Each puzzle consists of a grid of squares, and a collection of circles which are the centers of rotationally symmetric polyominoes which tile the grid. The puzzle is to determine the unique tiling with those centers. An example of a Spiral Galaxies puzzle and its solution are shown in Figure 1.

Figure 1. A Spiral Galaxies puzzle (left) and its solution (right)

We will show that the question of whether or not a given Spiral Galaxies puzzle has a solution is NP-complete. To do so, we construct Spiral Galaxies puzzles which correspond to arbitrary Boolean circuits. A circuit will be satisfied, (that is, have a set of inputs which give the desired outputs) if and only if the corresponding puzzle has a solution. Since Satisfiability is the canonical NP-complete problem [4], this will show that Spiral Galaxies puzzles are NP-hard. We complete the proof by showing that a solution to a Spiral Galaxies puzzle can be checked in polynomial time. Similar approaches to proving puzzles are NP-complete are taken in [1-3, 5-10].

To build a circuit, we first need wires capable of transmitting a signal of either TRUE or FALSE, variables which can take on either truth value, and outputs that force a particular truth value. Second, we need to construct logical gates: NOT, AND, and OR gates. Finally, we need a way of duplicating a signal, a way to allow wires to cross, and a way to shift the wires so that the gates can be connected correctly. From these building blocks, any given Boolean circuit can be constructed using Spiral Galaxies components.

Wires, Variables, and Outputs

Our wires will be rectangles of height 2 with a circle in the center of the wire between two squares every 3 units. Wires will always be horizontal, and signals will always travel from left to right. A wire carries the value TRUE if the local solution contains 2x3 rectangles, and the value FALSE if the local solution alternates 2x1 rectangles with 2x5 rectangles (see Figure 2).

Figure 2. Wires carrying signals of TRUE (left) and FALSE (right)

The variables are configurations at the start of wires whose only local solutions force a TRUE or FALSE signal in the wire. Our variables are shown in Figure 3.

Figure 3. Variables taking the values TRUE (left) and FALSE (right)

To force a particular truth value in an ouput wire, we simply terminate the wire at the appropriate point, as in Figure 4.

Figure 4. Outputs forcing values of TRUE (left) and FALSE (right)

NOT, AND, and OR Gates

Our NOT gate is two circles that are distance 2 apart, as shown in Figure 5.

Figure 5. NOT gates turning TRUE into FALSE (left) and FALSE into TRUE (right)

Our AND gate is shown in Figure 6. The inputs are on the top left and the output is on the bottom right. The rest of the local solution is forced by the inputs in each of the four cases. An OR gate can made from combining NOT gates with an AND gate.

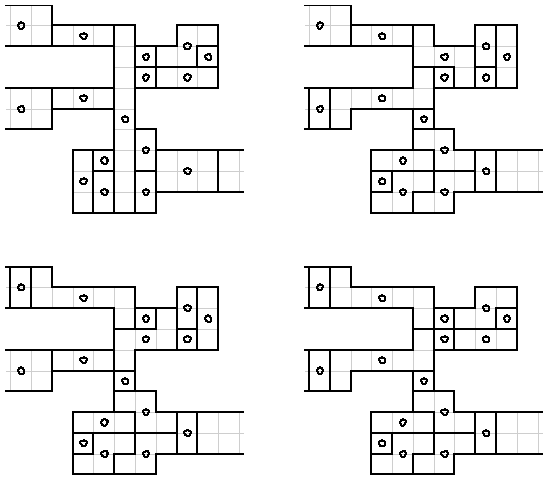
Figure 6. The four possible states of the AND gate

Crossing, Splitting, and Moving Wires

The configuration that allows two signals to cross is shown in Figure 7.

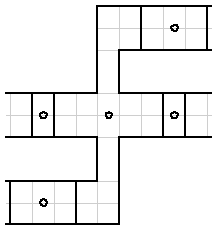
Figure 7. A TRUE signal crossing a FALSE signal

The configuration that duplicates a signal is shown in Figure 8. The input is on the top left and the outputs are on the right.

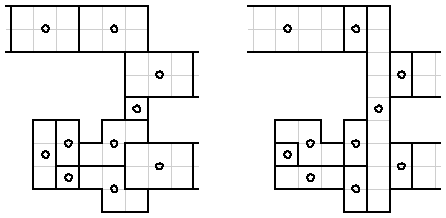
Figure 8. Duplicating a TRUE signal (left) and a FALSE signal (right)

A configuration to shift a signal one unit in any direction without changing the signal is shown in Figure 9.

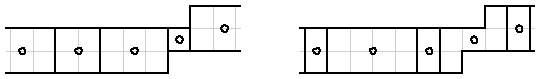
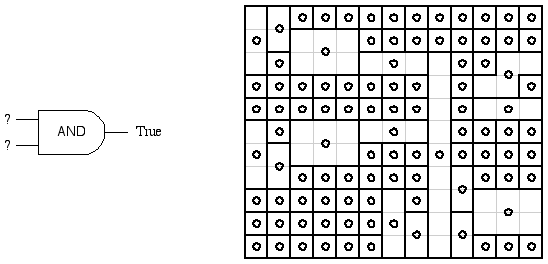
Figure 9. Shifting wires containing a TRUE signal (left) and a FALSE signal (right)

Spiral Galaxies puzzles are usually posed in rectangles (see Figure 1), but the circuit we have built from our wires and gates will only be some subset of a rectangle. This can be remedied by placing a circle in every grid square that is not part of our circuit. All the elements of our gates and wires are far enough apart that these additional circles allow only the trivial local solution. For example, a small circuit to be tested for Satisfiability and the corresponding solved Spiral Galaxies puzzle are shown in Figure 10.

Figure 10. An unsolved circuit (left) and its solved Spiral Galaxies puzzle (right)

Polynomial Time Checking

Assume that we are given a potential solution to a Spiral Galaxies puzzle as a list of grid squares in each polyomino. To verify that it is indeed a solution, for each grid square we need to find the location of the circle within the same polyomino, and determine whether the reflection of the grid square about the circle is in the same polyomino. This is clearly polynomial in the number of circles and the number of grid squares. Thus, in addition to being NP-hard, the problem of determining whether a Spiral Galaxies puzzle has a solution is NP-complete.

References

[1] D. Beauquier, M. Nivat, E. Rémila, and J.M. Robson, Computational Geometry 5 (1995) 1-25.
[2] J. Culberson, "Sokoban is PSPACE-complete." Proc. Internet Conf. Fun with Algorithms (1998), N. S. E. Lodi, L. Pagli, Ed., Carelton Scientific, 65-76.
[3] E. Friedman, "Cubic is NP-complete." preprint.
[4] M.R. Garey and D.S. Johnson, Computers and Intractibility: A Guide to the Theory of NP-Completeness. W.H. Freeman, 1979.
[5] E. Goles and I. Rapaport, "Complexity of tile rotation problems." Theoretical Computer Science 188 (1997) 129-159.
[6] E. Goles and I. Rapaport, "Tiling allowing rotations only." Theoretical Computer Science 218 (1999) 285-295.
[7] R. Kaye, "Minesweeper is NP-complete." Mathematical Intelligencer, to appear.
[8] K. Lindgren, C. Moore and M.G. Nordahl, "Complexity of two-dimensional patterns." Journal of Statistical Physics 91 (1998) 909-951.
[9] C. Moore and J.M. Robson, "Hard Tiling Problems with Simple Tiles." preprint.
[10] E. RŽmila, "Tilings with bars and satisfaction of Boolean formulas." Europ. J. Combinatorics 17 (1996) 485-491.