

Also of interest would be using identical rigid polykings in packing puzzles with unique solutions, up to rotation and reflection, such as the packing below.
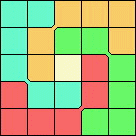
Both of these are somewhat trivial. Are there less trivial solutions?
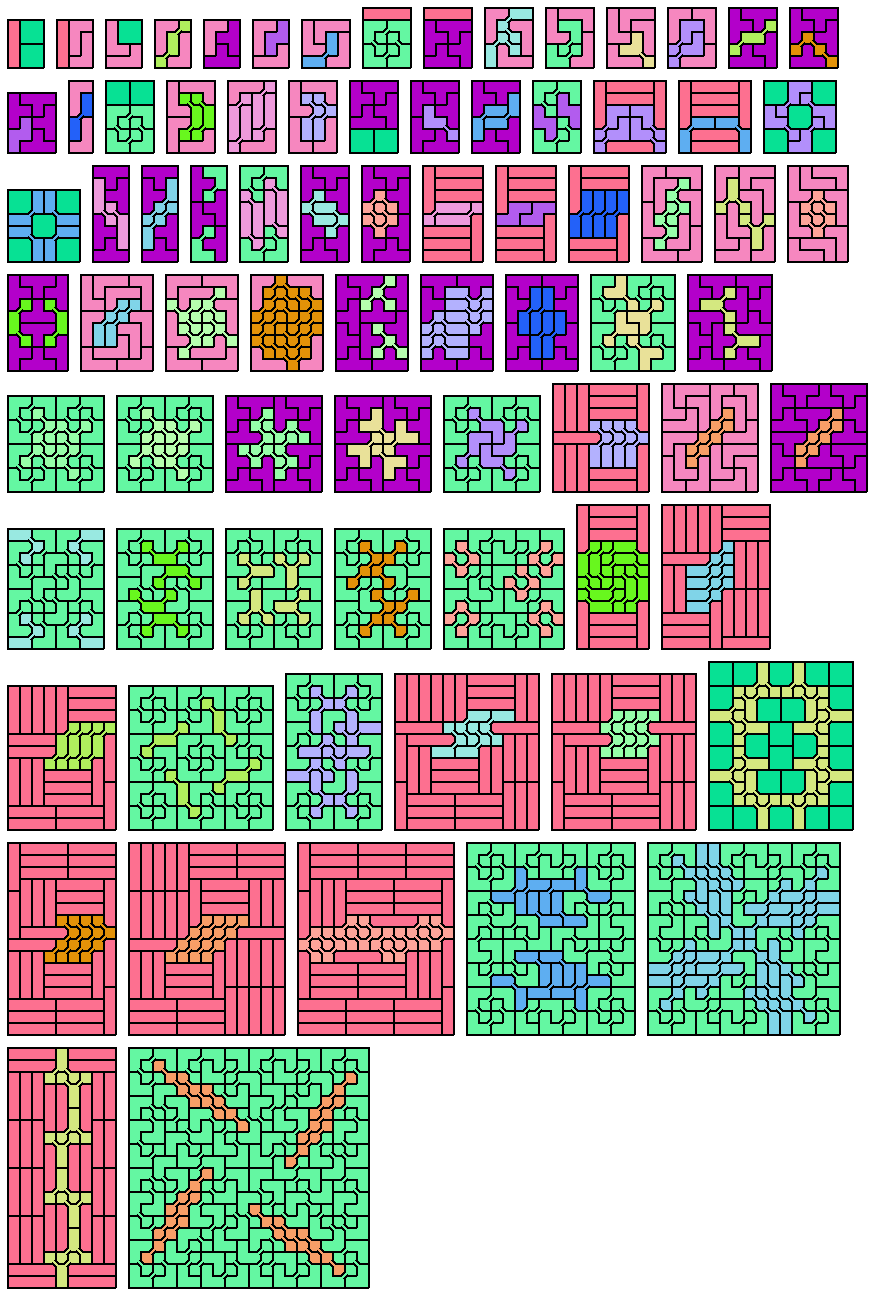
Here are the unique packings of tetrakings and pentakings that involve at least 3 of the tile:
| n \ m | 2 | 3 | 4 | 5 | 6 | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | none | none |
3    4 
5
| none
| 3 | 
3 |  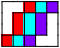 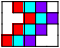 4    
3 |  4 
6
| none
| 3 |   
3 |  4   5   
5 |  6 
?
| 7
| none
| 3 |  
3 | 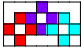 4  5   6    
 (GS) (GS)
?
| 8
| 3 | 
3 |   4 
5 |  6   7   
none
| ?
| |
| n \ m | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|
| 5 | none |
3 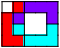 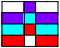   | 3       4      | ||
| 6 | 3  
| 3    | 3 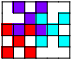 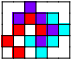  4 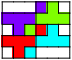 
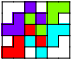 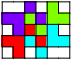 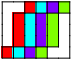
 5     
| 3 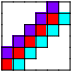 4    5   
| |
| 7 | 3  
| 3 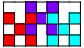  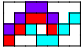 4    | 3 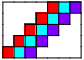 4  5      6     
| 5  6     7   (all GS) | 6  8   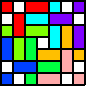
(all GS) |
| 8 | 3   | 3  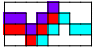 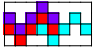 4     5  6 
| 4    5  6      7      (all GS) | 6  7   8    (all GS) | 7 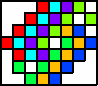 8 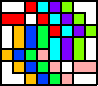   10   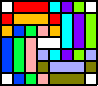 (all GS) |
| 9 | 3 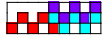  4  
| 3 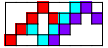  (GS) (GS)4    5  (GS) (GS)
| 5   6  7      8      (all GS) | 9  10  (all GS) | 10   (all GS) |
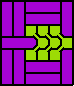
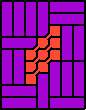
George Sicherman was interested in pairs of rigid polykings tiling rectangles:

| 
| 
| 
| 
| 
| 
|

|
|
If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 4/1/19.