The same question can be asked about circles packed in rectangles (the appropriate packing page for circles in squares is here, though you might also want to look at these animations). Let c(x,y) denote the maximum number of non-overlapping circles with diameter 1 that will fit inside an x × y rectangle. Let C_n denote the portion of the first quadrant with x≥1, y≥1, and with c(x,y)≤n. Then C₁ = { (x–1)²+(y–1)²<1 }. What is C₂? What are C_n for larger n? What about T_n for triangles?

Here are the results known for squares. The limiting packing shows how more squares can fit if you cross the boundary curve.

n	Boundary Curves of Sn	Limiting Packing	Largest Aspect Ratio	Author
1	x = 2		1
2	x = 3		(1+2√2)/6 = .638+
	x + 2y = 4 + 2√2		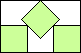1/√2 = .707+
	y = 2		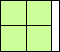1
3	x = 4		.470+
	{ x = 2 [ 2 – 3 t2 – t3 + (t2 – 2 t + 2)√(1 – t2) ] / (2 – 3 t2) y = 2 [ 1 – t2 – t3 + √(1 – t2)3 ] / (2 – 3 t2)		(1+2√2)/7 = .546+	(MM)
	y = 2		1
4	x = 5		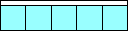(6√2–1)/20 = .374+	(MM)
	x + 4y = 4 + 6√2		(2+3√2)/14 = .445+	(MM)
	y = 2		2/3 = .666+	(MM)
	x = 3		(1+√2)/3 = .804+	(MM)
	x + y = 4 + √2		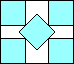1	(MM)
5	x = 6		.310+	(MM)
	{ x = 2 [ 3 – 2 t – 5 t2 - 2 t3 + 2(t2 – 2 t + 3)√(1 – t2) ] / (3 – 5 t2) y = 2 [ 1 – t2 - 2 t3 + 2 √(1 – t2)3 ] / (3 – 5 t2)		(3+4√2)/23 = .376+	(MM)
	y = 2		2/3 = .666+	(MM)
	x = 3		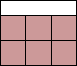1	(MM)
6	x = 7		(10√2–3)/42 = .265+	(MM)
	x + 6y = 4 + 10√2		(4+5√2)/34 = .325+	(MM)
	y = 2		1/2 = .500	(MM)
	x = 4		(1+√2)/4 = .603+	(MM)
	x + y = 5 + √2		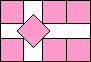(6–3√2)/2 = .878+	(MM)
	y = 3		1	(MM)
7	x = 8		.231+	(MM)
	{ x = 2 [ 4 – 6 t – 7 t2 – 3 t3 + 3(t2 – 2t + 4)√(1 – t2) ] / (4 – 7t2) y = 2 [ 1 – t2 – 3t3 + 3√(1 – t2)3 ] / (4 – 7t2)		(5+6√2)/47 = .286+	(MM)
	y = 2		1/2 = .500	(MM)
	x = 4		1/√2 = .707+	(MM)
	y6 – 10y5 + 29y4 – 8y3 – 48y2 + 64y + x4 – 16x3 + 48x2 – 64x + 2x2y3 – 14x2y2 + 40x2y – 64xy + 64 = 0		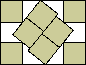.795+	(MM)
	(x–2)2 + (y–2)2 = 4		3(2–√3) = .803+	(MM)
	y = 3		1	(MM)
8	x = 9		(14√2–5)/72 = .205+	(MM)
	x + 8y = 4 + 14√2		(6+7√2)/62 = .256+	(MM)
	y = 2		2/5 = .400	(MM)
	x = 5		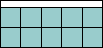(1+√2)/5 = .482+	(MM)
	x + y = 6 + √2		(2+6√2)/17 = .616+	(MM)
	x + 2y = 6 + 3√2		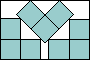1/√2 = .707+	(MM)
	y = 3		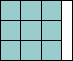1	(MM)
9	x = 10		.184+	(MM)
	{ x = 2(5 – 12t – 9t2 – 4t3 + 4 (t2 – 2t + 5)√(1 – t2))/(5 – 9t2) y = 2(1 – t2 – 4t3 + 4√((1 – t2)3))/(5 – 9t2)		(7+8√2)/79 = 0.231+	(MM)
	y = 2		2/5 = .400	(MM)
	x = 5		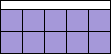2√2/5 = 0.565+	(MM)
	x + 2y = 5 + 4√2		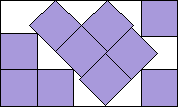3(1+4√2)/31 = 0.644+	(MM)
	y = 3		3/4 = 0.750	(MM)
	x = 4		(1+√5)/4 = 0.809+	(MM)
	x4 + y4 – 10x3 – 10 y3 + 20x2 + 20y2 + 8x + 8y – 2x2y2 + 10x2y + 10xy2 – 42xy – 32 = 0		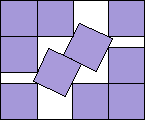(73 + 5√13-√(730√13 – 2446))/90 = 0.859+	(MM)
	(x – 3)2 + (y – 3)2 = 1		1	(MM)

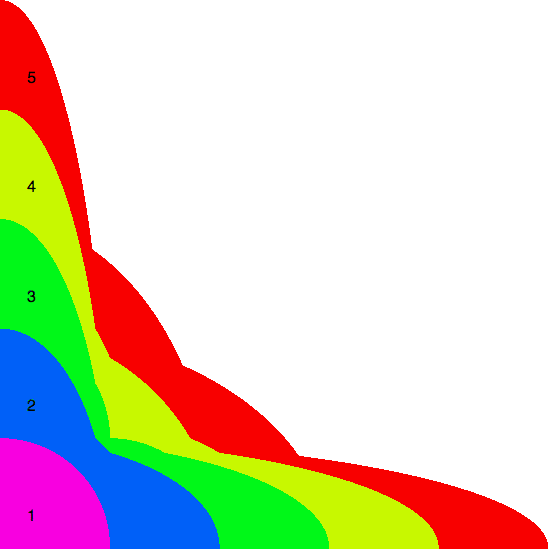
Here are the results known for circles. The limiting packing shows how one more circle can fit if you cross the boundary curve.

n	Boundary Curves of Cn	Limiting Packing	Largest Aspect Ratio	Author
1	(x–1)2 + (y–1)2 = 1		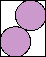1
2	(x–1)2 + 4(y–1)2 = 4		(2+√3)/4 = .933+
	(2x–2+√3)2 + (2y–2+√3)2 - 4√3 x y = (2–√3)2		1	(MM)
3	(x–1)2 + 9(y–1)2 = 9		(2+√3)/5 = .746+
	(x–2)2 + (y–1)2 = 1		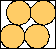1
4	(x–1)2 + 16(y–1)2 = 16		(2+√3)/6 = .622+
	4(x-1+√3)2 + (4y-4+√3)2 - 8√3(xy-1) = 19		√3–1 = .732+	(MM)
	(x–1)2 + (y–1)2 = 4		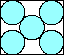1
5	(x–1)2 + 25(y–1)2 = 25		(2+√3)/7 = .533+
	(x–3)2 + (y–1)2 = 1		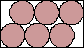2/3 = .666+
	(x–1)2 + 4(y–2)2 = 4		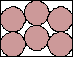5(√3–1)/4 = .915+
	4(x–1)2 + 9(y–1)2 = 36		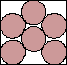1
6	(x–1)2 + 36(y–1)2 = 36		(2+√3)/8 = .466+
	(x–2+√3)2 + (2y–2+√3)2 - 2√3 x y = (2–√3)2		4-2√3 = .535+	(MM)
	2x – √[y (4 – y)] – 2 √[(1 + y)(3 – y)] = 2		(2+2√3)/(4+4√12) = .932+	(MM)
	4x – √3 y – 2 √[y (4 – y)] - √[(1 + y)(3 – y)] = 4 – √3		.981+	(MM)
	(x + 2y)(1 + √3) – x √[(y – 1)(3 – y)] + (1 – √3 – y + √[3 (y – 1)(3 – y)]) √[(x – 1)(3 – x)] - √3 x y = 3 + 2√3		1	(MM)
7	(x–1)2 + 49(y–1)2 = 49		(2+√3)/9 = .414+	(MM)
	(x–4)2 + (y–1)2 = 1		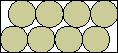1/2 = .500	(MM)
	(x–1)2 + 9(y–2)2 = 9		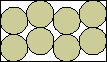5/(2+3√3) = .694+	(MM)
	21(x–1+2/√3)2 + (7y–7+2√3)2 – 28√3(xy – 1) = 103		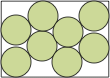(217+13√651)/(217+38√217) = .706+	(DC)
	(x–1)2 + 4(y–1)2 = 16		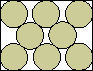(1+√3)/3 = .910+	(MM)
	(2x–2+√3)2 + (2y–2+√3)2 - 4√3 x y = 10 – 4√3		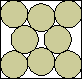1	(MM)
8	(x–1)2 + 64(y–1)2 = 64		(2+√3)/10 = .373+	(MM)
	4(x-3+√3)2 + (4y-4+3√3)2 – 8√3 x y = (3√3–4)2		1–1/√3 = .422+	(MM)
	x + 2y – (x – 1)√[(y – 1)(3 – y)] – (y – 1)√[(x – 1)(5 – x)] = 4		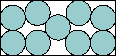(6+√3+3√((3+4√3)/13))/16 = .647+	(MM)
	(x – 1)√[(2y – √3)(4 + √3 – 2y)] + 2(y – 2)√[x (4 – x)] – x + 2(2 – √3)y = 5 – 2√3		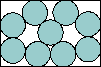.647+	(MM)
	2x – 5 = 2√[4–(y–1)2] + (y–1)√[(3–(y–1)2)/(1+(y-1)2)]		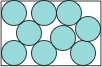.665+	(DC)
	4(x–1)2 + 25(y–1)2 = 100		2(1+√3)/7 = .780+	(MM)
	4(x–3)2 + (y–1)2 = 4		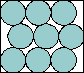1	(MM)
9	(x–1)2 + 81(y–1)2 = 81		(2+√3)/11 = .339+	(DC)
	(x–5)2 + (y–1)2 = 1		2/5 = .400	(DC)
	(x–1)2 + 16(y–2)2 = 16		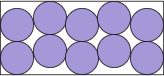5/(2+4√3) = .560+	(DC)
	9(x–1)2 + 16(y–2)2 = 144		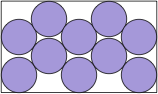.587+	(DC)
	(x–2)4 (8y2–20y+13) + 8(x–2)2 (y–1)2 (8y2–28y+17) + 16(y–1)4 (8y2–36y+37) = 0		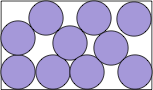.590+	(DC)
	very complicated		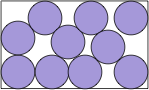2(1+√3)/7 = .596+	(DC)
	16(x–1)4 + 8(x–1)2 (17y2–36y–48) + (15y2–28y–48)2 = 0		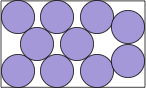(2+2√3)/(6+√(2√3)) = .695+	(DC)
	2(x–1) = √3(y–1) + √[(4–y)y] + √[(3–y)(1+y)]		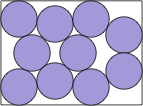.737+	(DC)
	very complicated		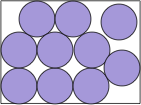(21+2√3)/33 = .741+	(DC)
	very complicated		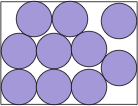.754+	(DC)
	256(y–1)8 + 128(x2–8x+4) (y–1)6 + 16(7x4–76x3+278x2–344x+144) (y–1)4 – 8(x–1) (x–4) (3x4–15x3–4x2+68x–64) (y–1)2 + (x–1)2 (x–4)2 (3x2–15x+16)2 = 0		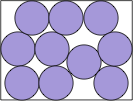(4+√(2√3))/(4+2√3) = .785+	(DC)
	very complicated		.801+	(DC)
	very complicated		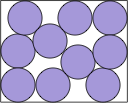.806+	(DC)
	x6 – 12x5 + 3x4 (y2–4y+22) – 8x3 (3y2–13y+28) + 3x2 (y4–8y3+44y2–128y+163) – 4x (3y4-26y3+96y2–184y+153) + y6 – 12y5 + 66y4 – 224y3 + 489y2 – 612y + 328 = 0		.812+	(DC)
	16(x–1)2 (x2–2x–2) + 16(8x2-16x+5)y – 4(10x2–20x–21)y2 – 96y3 + 21y4 = 8(x–1) (4x2–8x–2+8y-3y2) √[y(4–y)]		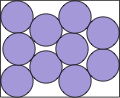6/(2+√3) = .833+	(DC)
	16(x–1)2 + 9(y–1)2 = 144		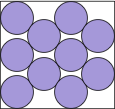.939+	(DC)
	very complicated		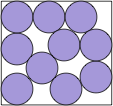(37+7√7)/57 = .974+	(DC)
	very complicated		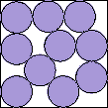1	(DC)
10	(x–1)2 + 100(y–1)2 = 100		(2+√3)/12 = .311+	(DC)
	(x–4+√3)2 + 4(y–1+√3)2 2√3(xy–4) = 16		2/(4+√3) = .348+	(DC)
	(x–2)4 (8y2–20y+13) + 2(x–2)2 (y–1) (40y3–212y2+337y–173) + 64(x–2) (y–3) (y–1)3 + (y–1)2 (72y4-660y3+2173y2–3022y+1501) = 0		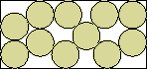.466+	(DC)
	(x–1)2 + 9(y–1)2 = 36		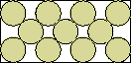(1+√3)/4 = .683+	(DC)
	(2x-4+√3)2 + 4(y-1+√3)2 4√3(xy–2) = 19		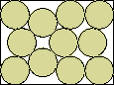6-3√3 = .803+	(DC)
	very complicated		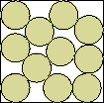.996+	(DC)
	very complicated		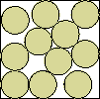1	(DC)
11	(x–1)2 + 121(y–1)2 = 121		(2+√3)/13 = .287+	(DC)
	(x–6)2 + (y–1)2 = 1		1/3 = .333+	(DC)
	(x–1)2 + 25(y–2)2 = 25		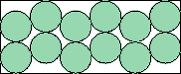5/(2+5√3) = .469+	(DC)
	9(x–1)2 + 25(y–1)2 = 225		.488+	(DC)
	4(3–y) (y–1) (7–5x+x2–8y+2xy+3y2)2 = (3–8x–x2+14y+8xy+2x2y–19y2–4xy2+6 y3)2		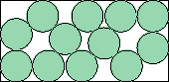(3744+675√3+√(630291+1332640√3))/13292 = .498+	(DC)
	(x–4)4 (8y2–20y+13) + 2(x–4)2 (y–1)2 (8y2–28y+17) + (y–1)4 (8y2–36y+37) = 0		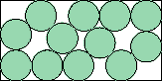.503+	(DC)
	2x – 5 = 4√[4-(y–1)2] + (y–1)√[(3–(y–1)2)/(1+(y–1)2)]		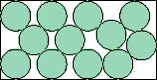.512+	(DC)
	4(x–1)2 + 49(y–1)2 = 196		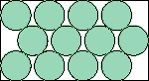2(1+√3)/9 = .607+	(DC)
	4(x–4)2 + (y–1)2 = 4		3/4 = .750	(DC)
	(x–1)2 + 9(y–3)2 = 9		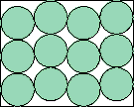7/(2+3√3) = .972+	(DC)
	25(x–1)2 + 9(y–1)2 = 225		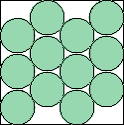1	(DC)

n	Boundary Curves of Tn	Limiting Packing	Largest Aspect Ratio	Author
1	x2 + y2 – √3xy = 1/4		1	(MM)
2	x2 + y2 = 3		1	(MM)
3	4y2 + 3x2 + 2√3xy – 9x – 6√3y + 6 = 0		(3√39 – 9√3)/4 = .786+	(MM)
	16x4 + 64x2y2 – 64√3yx2 – 8x2 + 1 = 0		3 – √2 + √3 – √6 = .868+	(MM)
	(2x – √3)2 + (2y – √3)2 = 3		1	(MM)
4	4y4 + 4y2x2 – 21y2 – 3x2 – 6√3xy + 36 = 0		.717+	(MM)
	3y + √3x = 4 + 2√3		1	(MM)

Here is a picture of the small C_n:

If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 2/26/19.