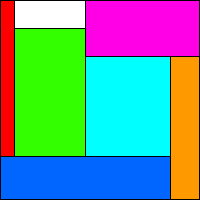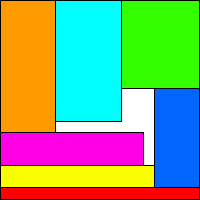Problem of the Month (August 1999)
This month we investigate 3 problems involving rectangles in squares.
Question #1:
Tile a square with area n(n+1)/2 with rectangles with area 1, 2, 3, . . . n so that the rectangles are as "square as possible". This is made precise below.
Define the aspect ratio of a rectangle to be the ratio of the smaller side to the bigger side. So the aspect ratio of a square is 1, and all other rectangles have aspect ratios smaller than 1. We want to tile a square with rectangles with areas 1, 2, 3, . . . n so that the smallest aspect ratio of the rectangles is as large as possible. Call this ratio R(n).
The sequence R(n) starts 1, 1/3, 1/2, . . . . What are the values of R(n) for larger n? Can you show that R(n) converges to 1 as n → ∞?
Question #2:
Pack n integer-sided rectangles in the smallest possible square so that no sides of rectangles are the same. Let S(n) be the side of the smallest square.
The sequence S(n) starts 2, 4, 6, 8, 11, . . . . What are the values of S(n) for larger n? Does S(n) / n3/2 converge as n → ∞?
Question #3:
Choose n points in a unit square so that the area of the largest unrotated rectangle that intersects none of the points is minimized. Let this minimum area be T(n).
The sequence T(n) starts 1/2, (3-√5) / 2, . . . What are the values of T(n) for larger n? How fast does T(n)->0 as n → ∞?
ANSWERS
Question #1:
Trevor Green gives these partial results:
Lemma: If R(n) ≥√(k/(k+1)), the rectangles 1,2, . . . , k do not share a complete edge with any other rectangle.
Corollary 1: If rectangle k shares a complete edge with another rectangle,
R(n) < √(k/(k+1)).
He uses these to get upper bounds on R(n) under the simplifying assumption that any time a rectangle is surrounded by 4 other rectangles, in such a way that none of them share an edge (he calls these windmills), these 5 rectangles form a rectangle. These upper bounds increase to 1 as n gets large.
Here are the best solutions found so far for R(n):
Largest Aspect Ratios
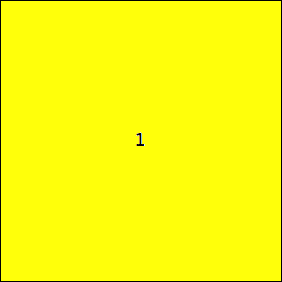
1
Trivial
| 
1/3 = .333+
Trivial
| 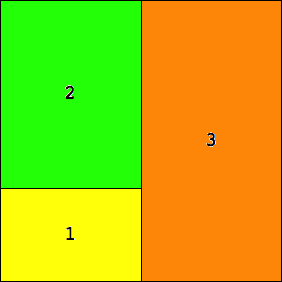
1/2 = .5
Trivial
|

8/15 = .533+
Joe DeVincentis
| 
64/135 = .474+
Erich Friedman
| 
64/105 = .609+
Erich Friedman
|

.614+
Maurizio Morandi
| 
.620+
Maurizio Morandi
| 
.675+
Erich Friedman
|

.671+
Maurizio Morandi
| 
361/528 = .683+
Maurizio Morandi
| 
147/208 = .706+
Erich Friedman
|

2548/3721 = .684+
Erich Friedman
| 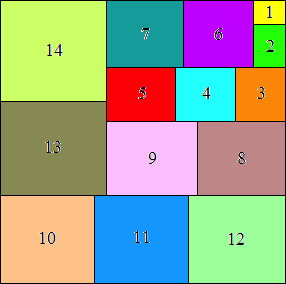
16384/23625 = .693+
Maurizio Morandi
| 
8281/12000 = .690+
Maurizio Morandi
|
Question #2:
From area considerations, S(n)2 must be at least A(n) = (1)(2n)+(2)(2n-1)+ . . . (n)(n+1) = n(n+1)(2n+1)/3. So S(n) ≥ √ 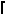 n(n+1)(2n+1)/3
n(n+1)(2n+1)/3 . In many small cases, this bound can be attained. It appears that S(n) ≤ √
. In many small cases, this bound can be attained. It appears that S(n) ≤ √  n(n+1)(2n+1)/3
n(n+1)(2n+1)/3 + 1. Trevor Green makes the following conjecture, which holds for n≤12.
+ 1. Trevor Green makes the following conjecture, which holds for n≤12.
Conjecture: Let S*(n) = √  A(n)
A(n)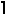 . Then S(n) is equal to S*(n) when S*(n)2 - S*(n) ≥ A(n) (and when n=4), and S*(n)+1 otherwise.
. Then S(n) is equal to S*(n) when S*(n)2 - S*(n) ≥ A(n) (and when n=4), and S*(n)+1 otherwise.
If this is true, A(n) = 2/3 × n3 + O(n2), S(n) = √(2/3) × n3/2 + O(n), so S(n) / n3/2 goes to √(2/3) as n gets large.
Here are the best known results for small n:
Smallest Square with n Rectangles

S(1)=2
Trivial
| 
S(2)=4
Trivial
| 
S(3)=6
Erich Friedman
| 
S(4)=8
Erich Friedman
|

S(5)=11
Erich Friedman
| 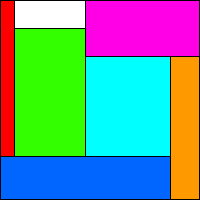
S(6)=14
Erich Friedman
| 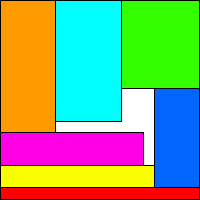
S(7)=18
Erich Friedman
| 
S(8)=21
Erich Friedman
|

S(9)=24
Maurizio Morandi
| 
S(10)=28
Maurizio Morandi
| 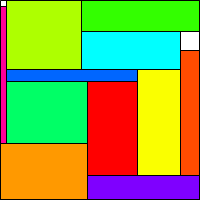
S(11)=32
Maurizio Morandi
| 
S(12)=37
Erich Friedman
|

S(13)=41
Maurizio Morandi
| 
S(14)=46
Erich Friedman
| 
S(15)=51
Erich Friedman
| 
S(16)=55
Sean Irvine
|
Question #3:
Here are the best solutions found so far:
Smallest Areas of Largest Rectangles

T(1) = 1/2 = .5
Trivial
| 
T(2) = (3-√5)/2 = .382+
Proved by Erich Friedman
| 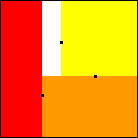
T(3) = .308+
Proved by Sasha Ravsky
| 
T(4) = 1/4 = .25
Proved by Sasha Ravsky
|

.211+ ≤ T(5) ≤ 2/9 = .222+
Found by Erich Friedman
| 
.179+ ≤ T(6) ≤ .196+
Found by Erich Friedman
| 
.174+ ≤ T(7) ≤ .173+
Found by Erich Friedman
| 
.159+ ≤ T(8) ≤ .158+
Found by Erich Friedman
|

.146+ ≤ T(9) ≤ .145+
Found by Erich Friedman
| .129+ ≤ T(10) ≤ .146+
Found by Sasha Ravsky
| .105+ ≤ T(11) ≤ .146+
Found by Sasha Ravsky
| .083+ ≤ T(12) ≤ .125+
Found by Sasha Ravsky
|
In 2007, I received the paper On Subsets Avoiding Large Rectangles by Sasha Ravsky. He proves several inequalities including 1/n ≤ T(n) and T(k2k-1) ≤ 1/2k.
If you can extend any of these results, please
e-mail me.
Click here to go back to Math Magic. Last updated 7/9/07.
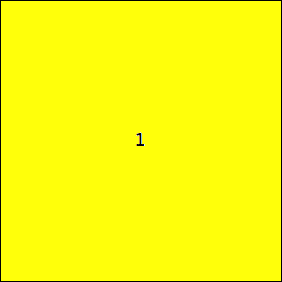














 n(n+1)(2n+1)/3
n(n+1)(2n+1)/3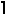 . In many small cases, this bound can be attained. It appears that S(n) ≤ √
. In many small cases, this bound can be attained. It appears that S(n) ≤ √