Problem of the Month (November 2019)

Last month we investigated Signatures of Rectangle Tilings by Various Sized Squares. This month we investigate a related problem, balanced tilings of rectangles by equal polyominoes. For a tiling of a rectangle with equal polyominoes, define its signature set to be the set of counts of how many polyominoes each polyomino is horizontally or vertically adjacent to. We call a tiling balanced if an equal number of polyominoes have each adjacency count in the signature set. For a given polyomino that can tile a rectangle, what signature sets have balanced tilings? What is the smallest such tiling?

ANSWERS

Contributions were received from George Sicherman and Joe DeVincentis.

1 and 2 Element Sets
12
1
2
3 none
1 and 2 Element Sets
123
1
2
3 none none
4 none
(GS)
5 none none
(JD)
(GS)
6 none none
(JD) 		none
(JD)
Others
{2,3,4}
{3,4,5}

(GS)
{2,3,4,5}

1 and 2 Element Sets
123
1
2
3 none none
(JD)
4 none none
(JD)
(GS)
5 none none
(JD)
(JD)
6 none none
(JD) 		none
(JD)
7 none none
(JD) 		none
(JD)
Others
{2,3,4}
{3,4,5}

(GS)
{2,3,4,5}

(GS) 		{3,4,5,6}

(GS)

1 and 2 Element Sets
123
1
2
3 none
(GS) 		none
(JD)
4 none none
(JD)
5 none none
(JD) 		none
(JD)
6 none none
(JD) 		none
(JD)
7 none none
(JD) 		none
(JD)
8 none none
(JD) 		none
(JD)

Others
{2,3,4}

(GS)
{2,3,5}
{3,4,5}

(GS)
{2,3,4,5}

(GS)

1 and 2 Element Sets
123
1 none
2 none
3 none none
(JD)
4 none none
(JD) 		none
(JD)
5 none none
(JD) 		none
(JD)
6 none none
(JD) 		none
(JD)
7 none none
(JD) 		none
(JD)
8 none none
(JD) 		none
(JD)

Others
{2,3,4}

(GS)
{2,3,4,5}

(GS)

1 and 2 Element Sets
1234
1
2
3 none none
(JD)
4 none
(GS)
(GS) 		?
5 none ?
(JD) 		?
6 none ? ? ?
7 none none ? ?
8 none none ? ?
9 none none ? ?

Others
{2,3,4}
{2,4,5}

(GS) 		{3,4,5}

(GS) 		{3,4,6}

(GS) 		{3,5,6}

(GS)
{2,3,4,5}

(GS) 		{2,3,4,6}

(GS) 		{2,4,5,6}

(GS) 		{3,4,5,6}

(GS)
{3,4,5,7}

(GS) 		{2,3,4,5,6}

(GS)

1 and 2 Element Sets
1234
1
2
3 none none
(JD)
4 none none
(JD) 		none
(JD) 		none
(JD)
5 none none
(JD) 		none
(JD) 		none
(JD)
6 none none
(JD) 		none
(JD) 		none
(JD)
7 none none
(JD) 		none
(JD) 		none
(JD)
8 none none
(JD) 		none
(JD) 		none
(JD)
9 none none
(JD) 		none
(JD) 		none
(JD)
10 none none
(JD) 		none
(JD) 		none
(JD)

Others
{1,3,4,5}
{3,4,5,7}

(GS)
{1,2,3,4,5}

1 and 2 Element Sets
1234
1
(GS)
2
(GS)
(GS)
3 none
(GS) 		?
4 none ? ? ?
5 none ? ? ?
6 none none
(JD) 		? ?
7 none none
(JD) 		? ?
8 none none
(JD) 		? none
(JD)
9 none none
(JD) 		none
(JD) 		none
(JD)
10 none none
(JD) 		none
(JD) 		none
(JD)

Others
{2,3,4}

(GS) 		{3,4,5}

(GS) 		{3,4,6}

(GS)
{3,4,5,6}

(GS) 		{3,4,5,6,7}

(GS)

1 and 2 Element Sets
1234
1
(GS)
2
(GS)
(GS)
3 none
(GS) 		none
(JD)
4 none none
(JD) 		? none
(JD)
5 none none
(JD) 		? none
(JD)
6 none none
(JD) 		? none
(JD)
7 none none
(JD) 		none
(JD) 		none
(JD)
8 none none
(JD) 		none
(JD) 		none
(JD)
9 none none
(JD) 		none
(JD) 		none
(JD)
10 none none
(JD) 		none
(JD) 		none
(JD)

Others
{2,3,4}

(GS) 		{2,4,5}

(GS) 		{3,4,5}

(GS)
{3,4,6}

(GS) 		{2,3,4,5}

(GS) 		{3,4,5,6}

(GS)
{2,3,4,5,6}

(GS) 		{3,4,5,6,7}

(GS)

1 and 2 Element Sets
1234
1
(GS)
2
(GS)
(GS)
3 none
(GS) 		none
(JD)
4 none none
(JD) 		? none
(JD)
5 none none
(JD) 		none
(JD) 		none
(JD)
6 none none
(JD) 		none
(JD) 		none
(JD)
7 none none
(JD) 		none
(JD) 		none
(JD)
8 none none
(JD) 		none
(JD) 		none
(JD)
9 none none
(JD) 		none
(JD) 		none
(JD)
10 none none
(JD) 		none
(JD) 		none
(JD)

Others

And then there's this one:


(GS)
George Sicherman suggested we look at tilings of infinite strips as well. We show the period of the thinnest strip, and of those, the smallest period that can be repeated horizontally.

{2}{3}{4}{2,3}{3,4}{3,5}{4,5}{3,6}{4,6}

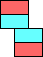
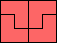
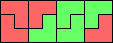
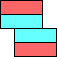
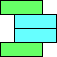
(GS)
(GS)
(GS)
(GS)
(GS)
(GS)
(GS)

(GS)
(GS)
(GS)
(GS)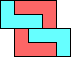
(GS)
(GS)
(GS)

(GS)
(GS)
(GS)
(GS)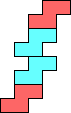
(GS)
(GS)
(GS)

(GS)
(GS)
(GS)
(GS)
(GS)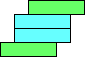
(GS)
(GS)
{2}{3}{4}{2,3}{3,4}{3,5}{4,5}{3,6}{4,6}

{2,3,4}{3,4,5}{3,4,6}{3,5,6}{4,5,6}{3,4,7}{4,5,7}{2,3,4,5}{3,4,5,6}{3,4,5,7}{3,4,6,7}{3,4,5,6,7}

(GS)
(GS)

(GS)
(GS)
(GS)

(GS)
(GS)
(GS)
(GS)

(GS)
(GS)
(GS)
(GS)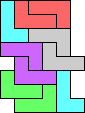
(GS)

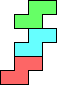(GS)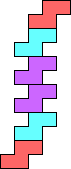
(GS)
(GS)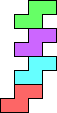
(GS)

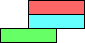(GS)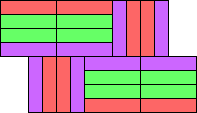
(GS)
(GS)
(GS)
(GS)
(GS)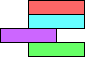
(GS)
(GS)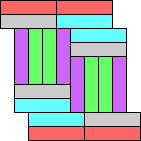
(GS)
{2,3,4}{3,4,5}{3,4,6}{3,5,6}{4,5,6}{3,4,7}{4,5,7}{2,3,4,5}{3,4,5,6}{3,4,5,7}{3,4,6,7}{3,4,5,6,7}

If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 11/1/19.